La formulaciion matemática fue publicada por Isaac Newton en 1687 en su obra Philosophiae Naturalis Principia Matemática.
Como sabemos, el movimiento es relativo, es decir, depende de cual sea el observador que describa el movimiento. Así, para un pasajero de un tren, el interventor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el interventor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento.
En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial.
-No hay formula; sólo F=0
Ejemplo:
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:
F = m a
F = m a
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea,
1 N = 1 Kg · 1 m/s2
La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo:un cohete que va quemando combustible, no es válida la relación F = m · a
. Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa.
Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:
p = m · v
La tercera ley, también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario.
Esto es algo que podemos comprobar a diario en numerosas ocasiones.
Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.
Cuando estamos en una piscina y empujamos a alguien, nosotros tambien nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros.
Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actuan sobre cuerpos distintos.
Ejercicios:
- 1. Una fuerza le proporciona a la masa de 2,5 Kg. una aceleración de 1,2 m/s2. Calcular la magnitud de dicha fuerza en Newton y dinas.
Datos
m = 2,5 Kg.
a =1,2 m/s2.
F =? (N y dyn)
Solución
Nótese que los datos aparecen en un mismo sistema de unidades (M.K.S.)
Para calcular la fuerza usamos la ecuación de la segunda ley de Newton:
Como nos piden que lo expresemos en dinas, bastará con multiplicar por 105, luego:
- 2. ¿Qué aceleración adquirirá un cuerpo de 0,5 Kg. cuando sobre él actúa una fuerza de 200000 dinas?
Datos
a =?
m = 2,5 Kg.
F = 200000 dyn
Solución
La masa está dada en M.K.S., en cambio la fuerza está dada en c.g.s.
Para trabajar con M.K.S. debemos transformar la fuerza a la unida M.K.S. de esa magnitud (N)

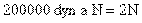
La ecuación de la segunda ley de Newton viene dada por:
- 3. Un cuerpo pesa en la tierra 60 Kp. ¿Cuál será a su peso en la luna, donde la gravedad es 1,6 m/s2?
Datos
PT= 60 Kp = 588 N
PL =?
gL = 1,6 m/s2
Solución
Para calcular el peso en la luna usamos la ecuación
Como no conocemos la masa, la calculamos por la ecuación: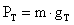 que al despejar m tenemos:
que al despejar m tenemos:
Esta masa es constante en cualquier parte, por lo que podemos usarla en la ecuación (I):

- 4. Un ascensor pesa 400 Kp. ¿Qué fuerza debe ejercer el cable hacia arriba para que suba con una aceleración de 5 m/s2? Suponiendo nulo el roce y la masa del ascensor es de 400 Kg.
Solución
Como puede verse en la figura 7, sobre el ascensor actúan dos fuerzas: la fuerza F de tracción del cable y la fuerza P del peso, dirigida hacia abajo.
La fuerza resultante que actúa sobre el ascensor es F – P
Aplicando la ecuación de la segunda ley de Newton tenemos:
Al transformar 400 Kp a N nos queda que:
400 Kp = 400 ( 9,8 N = 3920 N
Sustituyendo los valores de P, m y a se tiene:
F – 3920 N = 400 Kg. ( 0,5 m/s2
F – 3920 N = 200 N
Si despejamos F tenemos:
F = 200 N + 3920 N
F = 4120 N
- 5. Un carrito con su carga tiene una masa de 25 Kg. Cuando sobre él actúa, horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué magnitud tiene la fuerza de rozamiento Fr que se opone al avance del carrito?
Solución
En la figura 8 se muestran las condiciones del problema
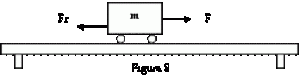
La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr, que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es la fuerza que produce el movimiento.
Si aplicamos la segunda ley de Newton se tiene:
Sustituyendo F, m y a por sus valores nos queda
80 N – Fr = 25 Kg. ( 0,5 m/s2
80 N – Fr = 12,5 N
Si despejamos Fr nos queda:
Fr = 80 N – 12,5 N
Fr = 67,5 N
- 6. ¿Cuál es la fuerza necesaria para que un móvil de 1500 Kg., partiendo de reposo adquiera una rapidez de 2 m/s2 en 12 s?
Datos
F =?
m = 1500 Kg.
Vo = 0
Vf = 2 m/s2
t = 12 s
Solución
Como las unidades están todas en el sistema M.K.S. no necesitamos hacer transformaciones.
De esa ecuación conocemos la masa, pero desconocemos la aceleración. Esta podemos obtenerla a través de la ecuación
Porque partió de reposo.
Sustituyendo Vf y t por sus valores tenemos:
Si sustituimos el valor de a y de m en la ecuación (I) tenemos que:

- 7. Calcular la masa de un cuerpo, que estando de reposo se le aplica una fuerza de 150 N durante 30 s, permitiéndole recorrer 10 m. ¿Qué rapidez tendrá al cabo de ese tiempo?
Datos
m =?
Vo = 0
F = 150 N
t = 30 s
x = 10 m
Vf =?
Solución
Como nos piden la masa, despejamos la segunda la segunda ley de Newton:

Como no se conoce la aceleración y nos dan la distancia que recorre partiendo de reposo, usamos la ecuación de la distancia en función del tiempo y despejamos (a)
Sustituyendo valores tenemos:
Sustituyendo los valores de X y t en (II) tenemos:
Tercera ley de newton.
- 1. Consideramos un cuerpo con un masa m = 2 Kg. que está en reposo sobre un plano horizontal, como el indicado en la figura 17. a) Haz un diagrama de cuerpo libre. b) Calcular la fuerza con que el plano reacciona contra el bloque.

Solución
a) Las fuerzas que actúan sobre el bloque están representadas en la figura 18, donde se elije un eje de coordenadas cuyo origen es el centro del cuerpo, mostrándose las fuerzas verticales: el peso y la normal
y la normal 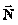
 y la normal
y la normal 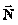
Al diagrama así mostrado se le llama diagrama de cuerpo libre.
b) Para calcular la fuerza que el plano ejerce sobre el bloque aplicamos la segunda ley de Newton:
Como  actúa hacia arriba y
actúa hacia arriba y 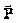 actúa hacia abajo, la resultante viene dada en módulo por N – P, que al aplicar la segunda ley de Newton escribimos:
actúa hacia abajo, la resultante viene dada en módulo por N – P, que al aplicar la segunda ley de Newton escribimos:
N – P = m . a
Como en la dirección vertical no hay movimiento entonces la aceleración es cero (a = 0), luego
N – P = 0
N = P
N = m . g (porque P = m ( g)
Sustituyendo los valores de m y g se tiene:
N = 2 Kg . 9,8 m/s2
N = 19,6 N
Esta es la fuerza con que el plano reacciona sobre el bloque.
- 2. En la figura 19 se muestran dos masas M1 = 3 Kg. y M2 = 5 Kg. colgando de los extremos de un hilo que pasa por la garganta de una polea a) Hacer un diagrama de las fuerzas que actúan b) Calcular la tensión del hilo y la aceleración con que se mueve el sistema.
Solución
a) Obsérvese la figura 20(a), la cual representa el diagrama del cuerpo libre para el cuerpo de masa M1.
En la figura 20(b) se muestra el diagrama de cuerpo libre para el cuerpo de masa M2.
b) Como el cuerpo de masa M1 sube, la tensión T es mayor que P, por lo que podemos escribir en módulo la segunda ley de Newton así:
T – P1 = M1 . a.………………………………………… (A)
Como el cuerpo de masa M2 baja, el peso P2 es mayor que T, pudiéndose escribir en módulo la segunda ley de Newton así:
P2 – T = M2 . a.………………………………………… (B)
Despajando T de la ecuación (A) nos queda que:
T = M1 . a + P1
Sustituyendo ésta expresión en (B) tenemos:
P2 – (M1 . a + P1) = M2 . a
P2 – P1 = M2 . a + M1 . a
Sacando a como factor común:
P2 – P1 = a . (M2 + M1)
Despejando nos queda:
Calculemos por separado P1 y P2
P1 = M1 . g = 3 Kg . 9,8 m/s2
P1 = 29,4 N
P2 = M2 . g = 5 Kg. . 9,8 m/s2
P2 = 49 N
Sustituyendo todos los valores conocidos en la expresión (C) nos queda que:
La tensión la obtenemos sustituyendo en la expresión:
T = M1 . a + P1
T = 3 Kg . 2,45 m/s2 + 29,4 N
T = 7,35 N + 29,4 N
T = 36,4 N
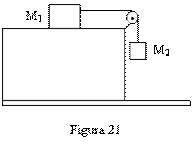
- 3. En la figura 21 se muestran dos bloques de masa M2 = 2 Kg. que arrastra sobre el plano horizontal al cuerpo de masa M1 = 7 Kg. Calcular la aceleración del sistema y tensión de la cuerda.
Solución
Antes debemos hacer un diagrama del cuerpo libre.
Para el bloque horizontal se muestra la figura 21(a) y para el bloque vertical el diagrama de la figura 21(b).

Horizontalmente se desplaza hacia la derecha y la única fuerza que actúa es la tensión, por lo que puede escribirse de acuerdo con la segunda ley de Newton que:
T = M1 . a.………………………….…………….….… (I)
En el bloque de masa M2, se lleva a cabo un movimiento vertical hacia abajo, pudiéndose escribir que:
P2 – T = M2 . a.………………………………………… (II)
Sustituyendo T de la ecuación (I) en (II) se tiene:
P2 – M1 . a = M2 ( a
Transponiendo términos se tiene que:
P2 = M2 . a + M1 ( a
Sacando a como factor común:
P2 = a . (M2 + M1)
Despejando nos queda:
Sustituyendo todos los valores conocidos en la expresión (C) nos queda que:
La tensión de la cuerda la obtenemos sustituyendo en la expresión:
T = M1 . a = 2Kg. ( 2,17 m/s2
T = 4,34 N
Ley de gravitación universal.
- 1. Hallar la fuerza con que se atraen dos masas de 5,5 ( 1024 Kg. y 7,3 ( 1022 Kg. separados por una distancia de 3,8 ( 108 m.
Solución
F = ?
M1 = 5,5 . 1024 Kg.
M2 = 7,3 . 1022 Kg.
d = 3,8 . 108 m
Para calcular la fuerza de atracción entre las masas M1 y M2, sustituimos en la fórmula de la cuarta ley de Newton el valor de cada una de ellas, así como los valores de G, y de la distancia d:
Quedando la fórmula como sigue:
- 2. Calcular la masa de un cuerpo, si fuerza de atracción entre dos masas es de 1,8 ( 10-2 N y la masa de una de ellas 0,6 ( 102 Kg., y las separa una distancia de 0,2 ( 10-1 m.
Solución
F = 1,8 ( 10-2 N
M1 = 0,6 ( 102 Kg.
M2 =?
d = 0,2 ( 10-1 m
Despejando M2 de la fórmula de la cuarta ley de Newton tenemos
Sustituyendo en la fórmula los valores tenemos:



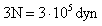



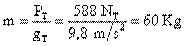
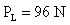


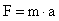

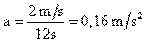

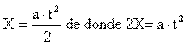
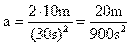
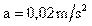








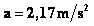
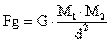



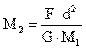
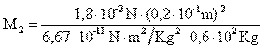
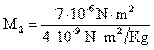

No hay comentarios.:
Publicar un comentario